고정 헤더 영역
상세 컨텐츠
본문
머신러닝 회귀 분석
project10. 환경에 따른 주택 가격 예측하기
- 핵심 개념: 머신러닝, 지도 학습, 사이킷런의 내장 데이터셋, 분석 평가 지표
- 데이터 수집: 보스턴 주택 가격 데이터 (사이킷런 내장 데이터셋)
- 데이터 준비 및 탐색
- 사이킷런 데이터셋 확인
- 사이킷런 데이터셋에 지정된 X 피처와 타깃 피처 결합
- 분석 모델 구축: 사이킷런의 선형 회귀 모델 구축
- 시각화
- 데이터가 주택 가격에 미치는 영향을 산점도와 선형 회귀 그래프와 시각화
1. 핵심 개념 이해
인공지능과 머신러닝
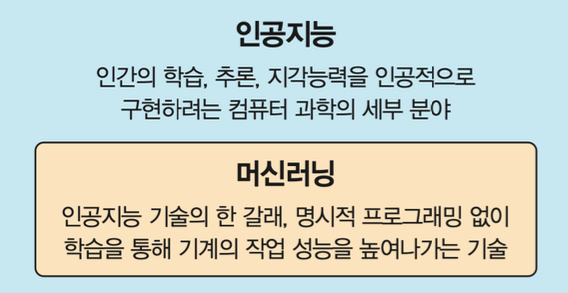
- 인공지능: 컴퓨터를 사용하여 인간의 지능을 구현하려는 기술
- 머신러닝: 인간이 지식과 경험을 학습하는 방법을 적용하여, 입력된 데이터에서 컴퓨터 스스로 패턴을 찾아 학습하여 새로운 지식을 만들고 예측하는 통찰(insight)을 제공하는 AI의 한 분야
머신러닝의 정의
- 아서 사무엘의 정의: 컴퓨터에 명시적인 프로그램 없이 스스로 학습할 수 있는 능력을 부여하는 연구 분야
- 톰 미첼의 정의: 컴퓨터 프로그램이 어떤 작업 T에 속한 일을 수행하면서 경험 E에 따라 P로 측정하는 성능이 개선되었다면, 이 프로그램은 작업 T와 성능 척도 P에 대해 경험 E로부터 학습된다고 할 수 있다.
톰 미첼의 정의

- 3가지 요소
T: 해결해야 할 문제(작업)
P: T를 수행하는 동작을 평가하는 성능 척도
E: 지속적인 훈련 경험
톰 미첼의 정의에 따른 예
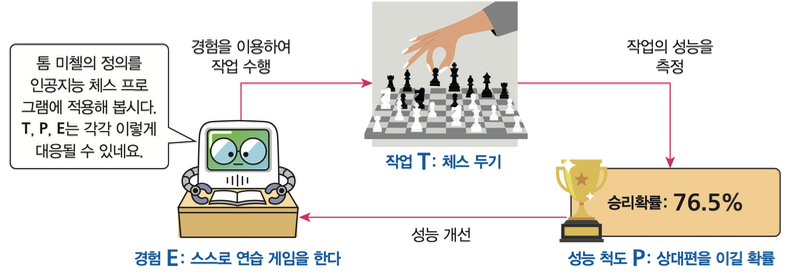
- 체스하는 컴퓨터 프로그램
작업 T: 체스를 한다.
성능 척도 P: 상대편을 이길 확률을 계산한다.
경험 E: 스스로 연습 게임을 한다.
-> 즉, 체스를 두는 작업(작업 T)을 하며 상대편을 이길 확률을 계산하고(성능 척도 P) 스스로 연습 게임을 하는 일을(경험 E) 바탕으로 성능 개선이 이루어진다면, 이 체스 프로그램은 머신러닝 알고리즘으로 동작한다고 말할 수 있다.
일반 프로그램 vs. 머신러닝
- 키가 160cm 이상인 사람만 이용 가능한 놀이기구가 있다고 가정

- 일반 프로그램으로 문제 해결
세 가지 구성 요소: 입력, 출력 그리고 명시적인 규칙을 가진 프로그램

- 머신러닝 프로그램으로 문제 해결
작업 T: 입장객의 키 데이터로 이용 가능/불가 고객의 기준 값을 찾음
성능 척도 P: 실제로 입장객이 놀이기구를 탄 확률
경험 E: 다양한 키 데이터로 작업하여 입장객이 놀이기구를 탄 확률이 높아지도록 기준값을 변경
선형 회귀
- 회귀(regression): 어딘가로 돌아간다는 의미
- 선형회귀(linear regression): 데이터들이 하나의 선으로 돌아간다. 즉, 하나의 선(y=ax+b)을 바탕으로 예측하는 것
- (예시01) 초록점들을 바탕으로 파란점의 위치 예측하기

1번 그림의 데이터를 통해서 데이터의 분포가 선형적인 상관관계를 가진다는 것을 알 수 있음
이를 통해, 2번 그림과 같은 y=2x 직선의 방정식을 유도할 수 있음
파란점의 y값이 '8'이라고 예측할 수 있음
- (예시02) 키와 몸무게의 관계: 키가 큰 사람이 작은 사람에 비해 몸무게가 많이 나갈 것이다.

키, 몸무게: 변수
두 변수가 함께 변화하는 관계: 상관관계
상관관계의 정도를 나타내는 수치: 상관계수
양의 상관 관계
이 데이터의 분포를 설명하는 직선: 선형 회귀 직선
이 직선의 함수: f(x) 선형 회귀 함수
선형 회귀는 실제 데이터를 바탕으로 새로운 데이터가 입력되었을 경우의 출력 결과를 예측할 수 있다.
- 앞의 예시에서 존재하는 데이터(초록점)를 바탕으로 어떻게 직선의 방정식(y=2x, 선형 회귀 방정식)을 얻었을까?
선형 회귀 직선의 기울기 2를 m으로 표기하고, 이 값을 구하는 문제로 생각해보자
| 이 모델은 선형 회귀 알고리즘
| m: 파라미터(parameter)
| 파란선의 길이: 오차(error)

- 직선이 오차를 줄이는 방향(1->2->3)으로 스스로 고쳐나가는 것을 수학적으로 '오차의 합이 점점 작이진다'고 하며, 곧 좋은 모델이 된다는 의미


- 회귀 분석 결과에 대한 평가 지표
예측값과 실제값의 차이인 오류의 크기
정확한 평가를 위해 오류의 절대값 평균, 제곱의 평균, 제곱 평균의 제곱근 또는 분산 비율을 사용
- 데이터의 분포를 가장 잘 설명하는 선형 회귀 직선을 구하는 과정을 최적화(optimization)
최적화 과정이 곧 머신러닝의 학습과정
머신러닝 학습 방법
- 기계에게 답을 알려주는 교사 역할의 여부에 따라 지도 학습과 비지도 학습으로 나뉨

- 지도 학습
교사에 의해 레이블 제공
레이블: 정답지 역할
대표적인 유형: 회귀와 분류
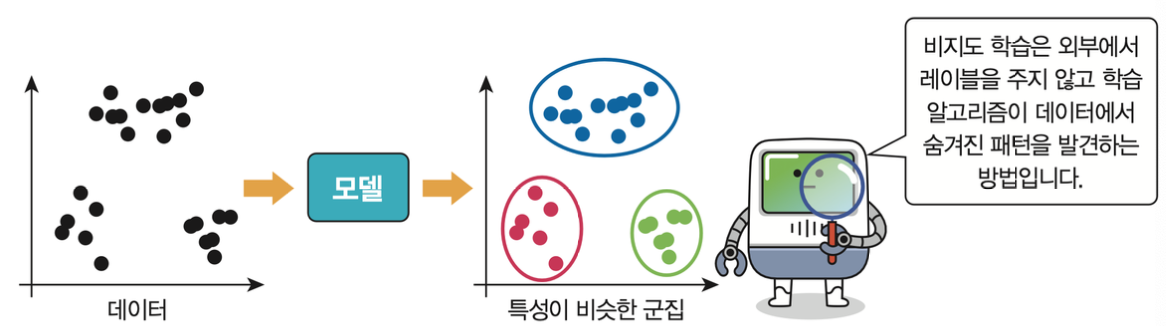
- 비지도 학습
데이터의 숨겨진 패턴 발견
대표적인 유형: 군집화


- 강화 학습: 보상을 통해 학습하는 방법
에이전트가 보상이 최대가 되는 방향으로 학습 수행
학습할 데이터를 사전에 주지 않아도 됨
예) 알파고, 로봇제어, 드론, 자율주행 자동차 운행 등 높은 수준을 보이는 프로그램에서 사용
사이킷런 라이브러리
- scikit-learn lib.
- 파이썬으로 머신러닝을 수행하기 위한 쉽고 효율적인 개발 라이브러리를 제공
- 보스톤 주택 가격 데이터, 붓꽃 데이터 등과 같은 머신러닝 분석용 데이터셋 제공
- 전체 n개의 컬럼 중 앞에서 (n-1)개의 컬럼은 독립 변수 X, 마지막 컬럼은 종속 변수 Y
- 데이터 표현 방식
특성 행렬(feature matrix)
| 입력 데이터
| 속성을 나타내는 독립변수
| [n_samples, n_features] 형태의 2차원 배열 구조
타겟 행렬(target matrix)
| 입력 데이터의 라벨(정답)을 의미
| 종속 변수
| [n_samples] 형태의 1차원 배열

2. 데이터 수집
- 사이킷런에서 제공하는 캘리포니아 주택 가격 데이터셋을 사용
!pip install scikit-learn #사이킷런 설치!pip install xlrdimport xlrd
import pandas as pd
test = pd.read_excel('cal_housing.xlsx', header=None)
test.head() #데이터 확인Out:

housing = pd.DataFrame(test[0].apply(lambda v: v.split(sep=',')).tolist(),
columns=('longitude', 'latitude', 'housingMedianAge', 'totalRooms',
'totalBedrooms', 'population', 'households', 'medianIncome', 'medianHouseValue'))
housing.info() #데이터프레임으로 변환한 데이터의 열 타입 확인Out:

housing = housing.astype(float) #데이터프레임 열과 타입을 str -> float 변환
housing.info() #다시 확인Out:

3. 데이터 준비 및 탐색
housing.head() #데이터 확인Out:

#열 totalRooms을 열 households(세대수)로 나눠서 새로운 AvgRooms 열을 생성
housing['AvgRooms'] = housing['totalRooms'].div(housing['households'], axis=0)
housing.head() #데이터 확인Out:

housing.shape
housing.info()Out:

4. 사이킷런의 선형 회귀 모델 구축
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
Y = housing['medianHouseValue']
X = housing.drop(['medianHouseValue'], axis=1, inplace=False)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=156)lr = LinearRegression() #선형 회귀 분석 모델 객체 lr 생성
lr.fit(X_train, Y_train) #training 데이터로 학습 수행
Y_predict = lr.predict(X_test) #선형 회귀 분석: test 데이터로 예측 수행 -> 결과 저장import numpy as np
mse = mean_squared_error(Y_test, Y_predict)
rmse = np.sqrt(mse)
print('MSE : {0:.3f}, RMSE : {1:.3f}'.format(mse, rmse))
print('R^2(Variance score) : {0:.3f}'.format(r2_score(Y_test, Y_predict)))Out:
MSE : 4931897011.667, RMSE : 70227.466
R^2(Variance score) : 0.632
print('Y 절편 값: ', lr.intercept_)
print('회귀 계수 값: ', np.round(lr.coef_, 1))Out:
Y 절편 값: -3724982.0992934047
회귀 계수 값: [-4.42596e+04 -4.40388e+04 1.19850e+03 -9.70000e+00 9.29000e+01
-3.69000e+01 7.67000e+01 3.95209e+04 2.03410e+03]
5. 시각화
import matplotlib.pyplot as plt
import seaborn as sns
fig, axs = plt.subplots(figsize = (16,16), ncols = 3, nrows = 3)
x_features = ['longitude', 'latitude', 'housingMedianAge', 'totalRooms', 'totalBedrooms', 'population', 'households', 'medianIncome', 'AvgRooms']
for i, feature in enumerate(x_features):
row = int(i/3)
col = i%3
sns.regplot(x=feature, y='medianHouseValue', data=housing, ax=axs[row][col])Out:

(추가) project 10-1. 데이터 크기 축소하여 산점도 표시하기
#데이터 축소 - housing2 산점도 표시하기
housing2 = pd.DataFrame(housing.loc[0:700])
housing2 = housing2.astype(float)
housing2.info()
housing2['AvgRooms'] = housing2['totalRooms'].div(housing2['households'], axis=0)
housing2.head()
housing2.shape
housing2.info()
Y2 = housing2['medianHouseValue']
X2 = housing2.drop(['medianHouseValue'], axis=1, inplace=False)
X_train2, X_test2, Y_train2, Y_test2 = train_test_split(X2, Y2, test_size=0.3, random_state=156)
lr2 = LinearRegression()
lr2.fit(X_train2, Y_train2)
Y_predict2 = lr.predict(X_test2)
mse2 = mean_squared_error(Y_test2, Y_predict2)
rmse2 = np.sqrt(mse2)
print('MSE2 : {0:.3f}, RMSE2 : {1:.3f}'.format(mse2, rmse2))
print('R^2(Variance score)2 : {0:.3f}'.format(r2_score(Y_test2, Y_predict2)))
coef = pd.Series(data = np.round(lr.coef_, 2), index = X.columns)
coef.sort_values(ascending = False)
fig, axs = plt.subplots(figsize = (16,16), ncols = 3, nrows = 3)
x_features = ['longitude', 'latitude', 'housingMedianAge', 'totalRooms', 'totalBedrooms', 'population', 'households', 'medianIncome', 'AvgRooms']
for i, feature in enumerate(x_features):
row = int(i/3)
col = i%3
sns.regplot(x=feature, y='medianHouseValue', data=housing2, ax=axs[row][col])Out:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 701 entries, 0 to 700
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 longitude 701 non-null float64
1 latitude 701 non-null float64
2 housingMedianAge 701 non-null float64
3 totalRooms 701 non-null float64
4 totalBedrooms 701 non-null float64
5 population 701 non-null float64
6 households 701 non-null float64
7 medianIncome 701 non-null float64
8 medianHouseValue 701 non-null float64
9 AvgRooms 701 non-null float64
dtypes: float64(10)
memory usage: 54.9 KB
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 701 entries, 0 to 700
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 longitude 701 non-null float64
1 latitude 701 non-null float64
2 housingMedianAge 701 non-null float64
3 totalRooms 701 non-null float64
4 totalBedrooms 701 non-null float64
5 population 701 non-null float64
6 households 701 non-null float64
7 medianIncome 701 non-null float64
8 medianHouseValue 701 non-null float64
9 AvgRooms 701 non-null float64
dtypes: float64(10)
memory usage: 54.9 KB
MSE2 : 5206763381.196, RMSE2 : 72157.906
R^2(Variance score)2 : 0.500

FIN.
'[SW] > 빅데이터 (2023) (완)' 카테고리의 다른 글
| [빅데이터 분석] 11. 머신러닝 분류 분석 (0) | 2023.07.25 |
|---|---|
| [빅데이터 분석] 09. 지리 정보 분석 II (0) | 2023.07.25 |
| [빅데이터 분석] 08. 지리 정보 분석 (0) | 2023.07.25 |
| [빅데이터 분석] 07. 텍스트 빈도 분석 (0) | 2023.07.25 |
| [빅데이터 분석] 06. 통계 분석II (1) | 2023.07.25 |






댓글 영역